
Technische Informationen: Tragfähigkeit & Lebensdauer
Für die Bestimmung der Lebensdauer bzw. Größe eines Kugellagers interessieren die Zusammenhänge zwischen der Lagerbelastung, Tragfähigkeit und Lebensdauer. Man unterscheidet zwischen der dynamischen Tragfähigkeit des umlaufenden Lagers und der statischen Tragsicherheit bei Belastung im Stillstand. Die nominelle Lebensdauer L10 und L10(h) beschreibt die dynamische Tragfähigkeit eines Wälzlagers. Der Faktor S0 die statische Sicherheit.
Dynamische Tragfähigkeit…
Bei einem umlaufenden Wälzlager besteht zwischen der Belastung und der Laufzeit des Lagers bis zur Werkstoffermüdung ein funktioneller Zusammenhang. Es treten beim Überrollen der Laufbahnen Wechselspannungen auf, die nach einer bestimmten Anzahl von Lastwechseln zur Ermüdung des Werkstoffes an der Oberfläche der Laufbahnen bzw. der Rollkörper führen. Die entsprechende Anzahl Umdrehungen bei einer bestimmten Belastung stellt die Lebensdauer eines Wälzlagers dar.
Die Berechnung der Lebensdauer erfolgt nach der Gleichung
L10(h) = 16.666/n · (C/P)3
Ihre graphische Auswertung zeigt die Netztafel. L10(h) und gibt dabei die Lebensdauer in Stunden bei 10% Ausfallwahrscheinlichkeit an.
Die Berechnung der Lebensdauer erfolgt nach der Gleichung
L10(h) = 16.666/n · (C/P)3
Ihre graphische Auswertung zeigt die Netztafel. L10(h) und gibt dabei die Lebensdauer in Stunden bei 10% Ausfallwahrscheinlichkeit an.
Auch kann die Tragfähigkeit eines Lagers für eine bestimmte Anzahl von Umdrehungen angegeben werden. Bei einer dynamischen Tragzahl C und einer dynamisch äquivalenten Belastung P wird eine nominelle Lebensdauer L10 von 106 Umdrehungen erreicht.
L10 = (C/P)3
Umgekehrt kann bei einer geforderten Lebensdauer in Stunden und bekannter Drehzahl sowie dynamisch äquivalenter Belastung die erforderliche, dynamische Tragzahl eines Lagers wie folgt bestimmt werden:
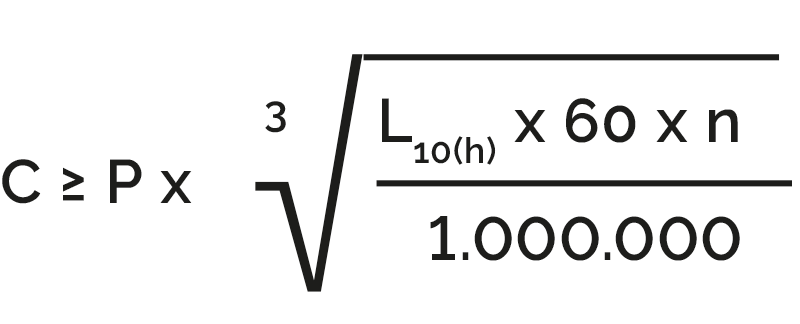
L10 = (C/P)3
Umgekehrt kann bei einer geforderten Lebensdauer in Stunden und bekannter Drehzahl sowie dynamisch äquivalenter Belastung die erforderliche, dynamische Tragzahl eines Lagers wie folgt bestimmt werden:
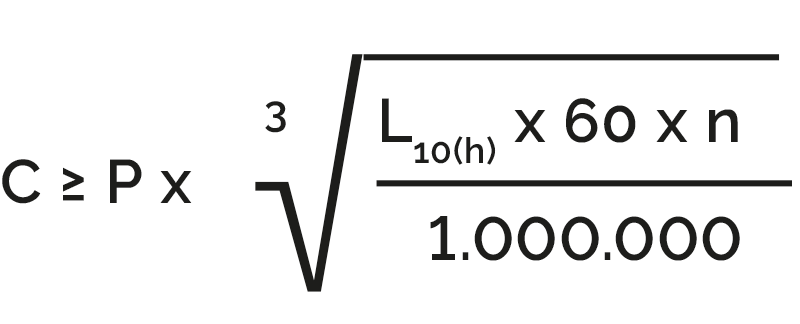
Statische Tragsicherheit…
Die statische Tragsicherheit S0 ist das Verhältnis aus der statischen Tragzahl C0 und der höchsten auftretenden Belastung P0.
S0 = C0 / P0
S0 = C0 / P0
| Betriebsbedingungen | Statische Tragsicherheit S0 |
|---|---|
| ruhiger, erschütterungsarmer Betrieb | ≥ 0,5 |
| normaler Betrieb | ≥ 1 |
| Betrieb bei Stoßbelastung | ≥ 2 |
| Lagerung mit hohen Ansprüchen an Laufgenauigkeit und Ruhe | ≥ 3 |
Äquiavalente Lagerbelastung…
Die äquivalente Lagerbelastung P ist eine, konstant in Größe und Richtung angenommene Belastung, die bei Radiallagern einer rein radialen Last entspricht. Diese hypothetische Last hat in der Anwendung dieselbe Auswirkung auf die Lagerlebensdauer wie die tatsächlichen Lasten, kombiniert aus axialen und radialen Komponenten.
Bei kombinierten Lastverhältnissen gilt es daher, die äquivalente Belastung für die Ermittlung der Lebensdauer oder statischen Sicherheit zu bestimmen. Bei rein radialer Belastung entspricht die äquivalente Belastung der radialen Belastung.
Die statisch äquivalente Belastung wird für Drehzahlen kleiner gleich 33 Umdrehungen pro Minute zugrunde gelegt. Sie wird zur Berechnung der statischen Sicherheit herangezogen.
Die dynamische äquivalente Belastung wird für Drehzahlen größer 33 Umdrehungen pro Minute zugrunde gelegt. Sie wird zur Berechnung der Lebensdauer herangezogen.
Für Radialkugellager gilt:
Dynamische äquivalente Belastung für Radial- und Schrägkugellager
P = XFr + YFa
Statische äquivalente Belastung für Radialkugellager
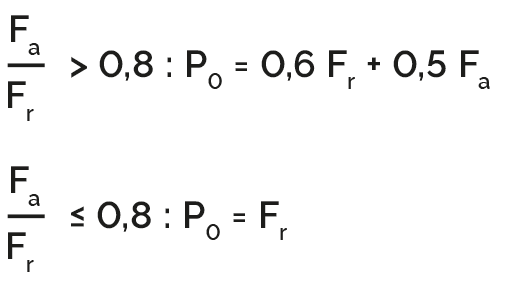
P = dynamische äquivalente Lagerlast
Po = statische äquivalente Lagerbelastung
fo = Faktor zur Berechnung der statischen Tragzahl
Fr = radiale Belastung in [N]
Fa = axiale Belastung in [N]
X = Radialfaktor des Lagers
Y = Axialfaktor des Lagers
C0r = statische Tragzahl
e = Weibull-Exponent
Dynamische äquivalente Belastung für Radial- und Schrägkugellager
P = XFr + YFa
Statische äquivalente Belastung für Radialkugellager
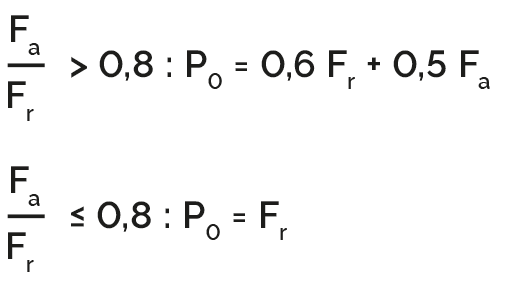
P = dynamische äquivalente Lagerlast
Po = statische äquivalente Lagerbelastung
fo = Faktor zur Berechnung der statischen Tragzahl
Fr = radiale Belastung in [N]
Fa = axiale Belastung in [N]
X = Radialfaktor des Lagers
Y = Axialfaktor des Lagers
C0r = statische Tragzahl
e = Weibull-Exponent
| Lagerluft Normal | |||||
|---|---|---|---|---|---|
| Fa/Fr ≤ e | Fa/Fr > e | ||||
| f0*Fa/C0r | e | X | Y | X | Y |
| 0,172 | 0,19 | 1 | 0 | 0,56 | 2,30 |
| 0,345 | 0,22 | 1 | 0 | 0,56 | 1,99 |
| 0,689 | 0,26 | 1 | 0 | 0,56 | 1,71 |
| 1,03 | 0,28 | 1 | 0 | 0,56 | 1,55 |
| 1,38 | 0,30 | 1 | 0 | 0,56 | 1,45 |
| 2,07 | 0,34 | 1 | 0 | 0,56 | 1,31 |
| 3,45 | 0,38 | 1 | 0 | 0,56 | 1,15 |
| 5,17 | 0,42 | 1 | 0 | 0,56 | 1,04 |
| 6,89 | 0,44 | 1 | 0 | 0,56 | 1,00 |
| Druckwinkel | Einzellager | gepaart DB oder DF | |
|---|---|---|---|
| 15° |
Fa/Fr ≤ 0,55 Fa/Fr > 0,55 |
P = Fr P = 0,45 Fr + Fa |
P = Fr + 1,25 Fa P = 0,72 Fr + 1,63 Fa |
| 25° |
Fa/Fr ≤ 0,68 Fa/Fr > 0,68 |
P = Fr P = 0,41 Fr + 0.87 Fa |
P = Fr + 0.92 Fa P = 0,66 Fr + 1,41 Fa |
| 30° |
Fa/Fr ≤ 0,80 Fa/Fr > 0,80 |
P = Fr P = 0,39 Fr + 0.76 Fa |
P = Fr + 0.78 Fa P = 0,63 Fr + 1,24 Fa |
| 40° |
Fa/Fr ≤ 1,14 Fa/Fr > 1,14 |
P = Fr P = 0,35 Fr + 0.57 Fa |
P = Fr + 0.55 Fa P = 0,56 Fr + 1,93 Fa |
| 45° |
Fa/Fr ≤ 1,35 Fa/Fr > 1,35 |
P = Fr P = 0,33 Fr + 0.5 Fa |
P = Fr + 0.46 Fa P = 0,53 Fr + 0,81 Fa |
